Question

The roots of \[z^7 = -\frac{1}{\sqrt{2}} - \frac{i}{\sqrt{2}}\]are $\text{cis } \theta_1$, $\text{cis } \theta_2$, $\dots$, $\text{cis } \theta_7$, where $0^\circ \le \theta_k < 360^\circ$ for all $1 \le k \le 7$. find $\theta_1 + \theta_2 + \dots + \theta_7$. give your answer in degrees.

Answer 1

Decoding the LaTeX that didn't render, we seek sum of the angles of the seventh roots of

`- \frac 1 {\sqrt 2} - \frac i {√(2)}`

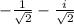
That's on the unit circle, 45 degrees into the third quadrant, aka 225 degrees.

The seventh roots will all be separated by 360/7, around 51 degrees. The first seventh root has

`\theta_1 = 225^\circ / 7`

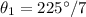
That's around 32 degrees.

The next angle is

`\theta_2 = (1)/(7)( 225^\circ + 360^\circ)`

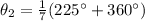
The next one is

`\theta_3 = (1)/(7)( 225^\circ + 720^\circ)`

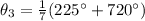
and in general

`\theta_n = (1)/(7)( 225^\circ + (n-1)360^\circ) = \frac 1 7(-135^\circ + 360^\circ n)`

`S = \displaystyle \sum_(n=1)^7 \theta_n = (1)/(7) \sum_(n=1)^7 -135^\circ + (360)/(7) \sum_(n=1)^7 n`

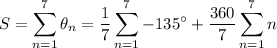
The first sum is just -135° since it's one seventh of the sum of seven -135s.

We have 1+2+3+4+5+6+7 = (1+7)+(2+6)+(3+5) + 4 = 28 so

`S = -135^\circ + 360^\circ (\frac{28} 7) = 4(360)-135 = 1305^\circ`

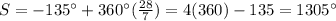
If I didn't screw it up, that means the answer is

Answer: 1305°