Question

Function = y=(x-4)^2-5+7

Calculate the x and y values for the vertex point of the parabola.
State what the axis of symmetry is.
Set your quadratic function to zero (let y = 0) and use either the quadratic formula or completing the square method to solve for the two solutions of x when y = 0
Calculate the discriminant for the quadratic equation.

Answer 1

Given equation of parabola is
`y=(x-4)^2-5+7`

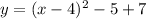
Or we can simplify that to
`y=(x-4)^2+2`

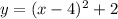
This equaion looks similar to formula
`y=a(x-h)^2+k`

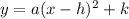
Comparing both equation, we get:

a=1, h=4, k=2

(h,k) represents the vertex of the parabola

Hence vertex of the given parabola is (4,2).

So x-value of the vertex = 4

So y-value of the vertex = 2

Axis of symmetry is given by equation x=h

So the answer will be x=4

Now we will set y=0 and solve this using quadratic formula including desriminant

`0=(x-4)^2+2`

`0=x^2-8x+16+2`

`0=x^2-8x+18`

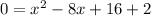
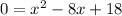
compare with quadratic equation
`0=ax^2+bx+c`, we get:

a=1, b=-8, c=18

Descriminant is given by formula:

`Descriminant = √(b^2-4ac) = √((-8)^2-4(1)(18))= √(-8)= -2√(2) i`

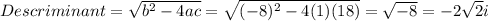
which is imaginary

Hence there will be no real solution for x-intercept.