To three decimal places, find the value of the first positive x-intercept for the function f(x) = 2cos(x + 4) 1.712 0.712 –2.429 –2.712

Question

asked Jan 18, 2019 168k views

2 Answers

Saxon Druce · Answer 1 · 2019-01-23T10:24:35+0000

Answer:

The correct option is B.

Explanation:

The given function is

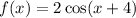
$f(x)=2\cos(x+4)$

We need to find the first positive x-intercept for the function f(x).

Equate f(x)=0, to find the x-intercepts.

f(x)=0

$2\cos(x+4)=0$

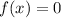
Divide both sides by 2.

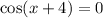
$\cos(x+4)=0$

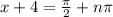
$x+4=(\pi)/(2)+n\pi$
$[\because \cos x=0, then x=(\pi)/(2)+n\pi,n\in Z]$

Subtract 4 from both sides.

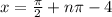
$x=(\pi)/(2)+n\pi-4$

For n=-1,

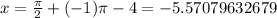
$x=(\pi)/(2)+(-1)\pi-4=-5.57079632679$

For n=0,

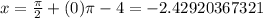
$x=(\pi)/(2)+(0)\pi-4=-2.42920367321$

For n=1,

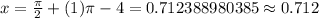
$x=(\pi)/(2)+(1)\pi-4=0.712388980385\approx 0.712$

The first positive x-intercept for the function f(x) is 0.712. Therefore the correct option is B.