Question

DATE

CLASS
14. The Space Shuttle must achieve a velocity of 7,800 m/s in order to orbit the
Earth If the average acceleration of the Space Shuttle is 15.3 m/s², how long will
It take for the shuttle to reach orbital velocity? Convert your answer from seconds
to minutes. Show all your work for this calculation.

Answer 1

8.49673 minutes ≈ 8.5 minutes

Step-by-step explanation:

Acceleration, a is defined as the rate of change in velocity divided by the change in time to attain that velocity

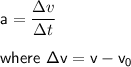`\mathsf a = (\Delta v)/(\Delta t) \\\\\textsf {where } \mathsf {\Delta v = v-v_0} \textsf{ v being final velocity and v_0 initial velocity}`, v = final velocity and v₀ the initial velocity
and Δt is the time required to attain final velocity

Δt = number of seconds since launch = t since t₀ = 0

Therefore,

`a = (v-v_0)/(t)`

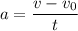
The space shuttle's initial velocity is 0 m/s and its final velocity must be 7800 m/s to escape earth's gravity

So v - v₀ = 7800 - 0 = 7800 m/s, t - t₀ = t = 0 = t seconds
a = 15.3 m/s²

We have the equation

a = 7800/t

a is given as 15.3 m/s² so
15.3 = 7800/t

t = 7800/15.3 = 509.80392 seconds

To convert to minutes, divide by 60
509.80392/60 = 8.49673 minutes ≈ 8.5 minutes