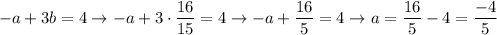Question

(b) find real numbers a and b such that (a, 2,

b.is orthogonal to both (−1, −2, 3) and (3, −2, 6).

Answer 1

Two vectors are orthogonal if their scalar product is zero. The scalar product of two vectors is computed as follows:

`(a_1,a_2,\ldots,a_n) \cdot (b_1,b_2,\ldots,b_n) = a_1b_1 + a_2b_2 + \ldots + a_nb_n`

In other words, you multiply each component of the first vector with the correspondant component of the second vector, and then you sum all these products.

So, we need to compute the two scalar products, and set them to zero:

`(a, 2,b) \cdot (-1, -2, 3) = 0 \iff -a-4+3b = 0`

`(a, 2,b) \cdot (3, -2, 6) = 0 \iff 3a-4+6b = 0`

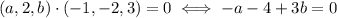
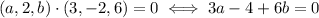
We can rewrite the two requests in this linear system:

`\begin{cases} -a+3b = 4\\3a+6b = 4 \end{cases}`

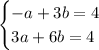
From the first equation we can deduce
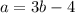`a = 3b-4`, which substituted in the second gives

`3a+6b = 4 \to 3(3b-4)+6b = 4 \to 9b-12+6b = 4 \to b = (16)/(15)`

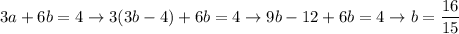
If we substitute this value for b in the first equation we have

`-a+3b = 4 \to -a+3\cdot (16)/(15) = 4 \to -a+(16)/(5) = 4 \to a = (16)/(5)-4= (-4)/(5)`