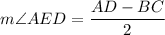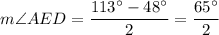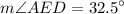Question

I need help on my homework

Answer 1

`\displaystyle m\angle AED=32.5^\circ`

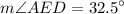
Explanation:

Angles in a Circle

An exterior angle of a circle is an angle whose vertex is outside a circle and the sides of the angle are secants or tangents of the circle.

Segments AE and DE are secants of the given circle. They form an exterior angle called AED.

The measure of an exterior angle is equal to half the difference of the measure of their intercepted arcs.

Intercepted arcs in the given circle are AD=113° and BC=48°. The exterior angle is:

`\displaystyle m\angle AED=(AD-BC)/(2)`

`\displaystyle m\angle AED=(113^\circ-48^\circ)/(2)=(65^\circ)/(2)`

`\displaystyle m\angle AED=32.5^\circ`