From given picture we can see that X is mid point of line PQ
So PQ=2PX
From given picture we can see that Y is mid point of line PR
So PR=2PY
Now consider triangles PRQ and PYX
Sides PQ and PX has same ratio as of sides PR and PY (as calculated above)
angle XPY= angle QPR (common angle)
Hence triangles PRQ and PYX are similar.
We know that ratio of the sides of similar triangles is always equal so we can write:
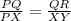
Plug the given values QR=8 and PQ=2PX
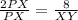
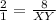
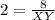
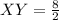
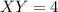
Hence final answer is XY = 4 units.