Question

Find the value of this expression: sin 45 sin 15 . The second step =

a. 1 sin 60 – sin 30 2
b. 1 cos 60 cos 30 2
c. 1 sin 60 sin 30 2
d. 1 cos 60 cos 30

Find the value of this expression: cos 75 – cos 15 . The second step =
a. –2 cos 45 cos 30
b. –2 sin 45 sin 30
c. 2 sin 45 cos 30
d. 2 cos 45 sin 30

Answer 1

Given expression is sin(45)sin(15)

this expression best matches with left side of the formula:

2 sin(A) sin(B)= cos(A-B) - cos(A+B)

so we can plug given angles 45 and 15 there

2 sin(45) sin(15)= cos(45-15) - cos(45+15)

2 sin(45) sin(15)= cos(30) - cos(60)

sin(45) sin(15)= [cos(30) - cos(60)]/2

We are getting negative sign and cos in the solution while none of the given choices have same situation so answer will be none of them.

-----------

For cos(75)-cos(15), we will use formula:

`\cos\left(A\right)-\cos\left(B\right)=-2\sin\left((A+B)/(2)\right)\sin\left((A-B)/(2)\right)`

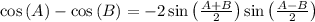
Now plug the given angles

`\cos\left(75\right)-\cos\left(15\right)=-2\sin\left((75+15)/(2)\right)\sin\left((75-15)/(2)\right)`

`\cos\left(75\right)-\cos\left(15\right)=-2\sin\left((90)/(2)\right)\sin\left((60)/(2)\right)`

`\cos\left(75\right)-\cos\left(15\right)=-2\sin\left(45\right)\sin\left30\right)`

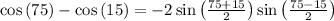
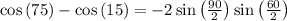
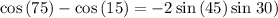
Hence choice B is correct.