So firstly, we have to find the radius of the circular garden before finding the circumference (the amount of fencing needed to surround the garden). To find the radius, use the area formula (
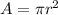 ), plug in the area of the garden (36 ft^2) and solve for r as such:
), plug in the area of the garden (36 ft^2) and solve for r as such:
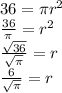
So that we know the radius, plug that into the circumference equation (
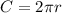 ) to solve:
) to solve:
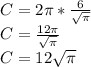
Your answer is A. 12√π.