Question

If pq=23 and uv= 1/23 find the value of (u)(q)(v)(p). Explain which properties you used.

Answer 1

The value of (u)(q)(v)(p) is 23*(1/23) = 1.

Note that the multiplicands in (u)(q)(v)(p) can be arranged in any order without affecting the final outcome (product). (u)(q)(v)(p), in this sense, is exactly the same as pq*uv, or just pquv, or (pq)*(uv).

The rule that applies here is the commutative rule for multiplication.

Answer 2

Answer with Step-by-step explanation:

The commutative property of multiplication says that if a and b are two elements

Then, ab=ba

(u)(q)(v)(p)

=(u)(v)(q)(p) (Using the commutative property (q)(v)=(v)(q))

=(u)(v)(p)(q) (Using the commutative property (q)(p)=(p)(q))

=
`(1)/(23)* 23`

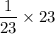
=1

Hence, the value of (u)(q)(v)(p) is:

1

and the property used is commutative property of multiplication