Answer:
Option 3rd is correct
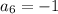
Explanation:
The nth term for the geometric sequence is given by:
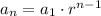
where,
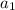 is the first term
is the first term
r is the common ratio
n is the number of terms.
As per the statement:
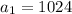
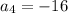
For n = 4, we have;
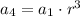
⇒
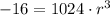
Divide both sides by 1024 we have;
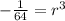
⇒
![r =\sqrt[3]{-(1)/(64)}=\sqrt[3]{-(1)/(4^3)}](https://img.qammunity.org/2019/formulas/mathematics/college/enuho265bf8yb5iuxmhojcn22plr3mak8g.png)
⇒
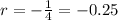
We have to find the value of 6th term.
for n = 6
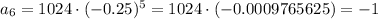
⇒
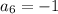
Therefore, the 6th term of the geometric sequence is, -1