So since the vertex falls onto the axis of symmetry, we can just solve for that to get the x-coordinate of both equations. The equation for the axis of symmetry is
 , with b = x coefficient and a = x^2 coefficient. Our equations can be solved as such:
, with b = x coefficient and a = x^2 coefficient. Our equations can be solved as such:
y = 2x^2 − 4x + 12:
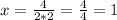
y = 4x^2 + 8x + 3:
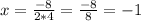
In short, the vertex x-coordinate's of y = 2x^2 − 4x + 12 is 1 while the vertex's x-coordinate of y = 4x^2 + 8x + 3 is -1.