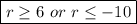Question

Solve the inequality. Show your work. |4r + 8| ≥ 32

Answer 1

`|4r+8|\geq32\iff4r+8\geq32\ \vee\ 4r+8\leq-32\ \ \ |-8\\\\4r\geq24\ \vee\ 4r\leq-40\ \ \ |:4\\\\r\geq6\ \vee\ r\leq-10`

`Answer:\ r\geq6\ \vee\ r\leq-10\to r\in\left(-\infty;\ -10\right>\ \cup\ \left< 6;\ \infty\right)`

Answer 2

|4r + 8| ≥ 32

Split this expression into two expressions:

First ⇒ 4r + 8 ≥ 32 and second ⇒ 4r + 8 ≤ - 32

---

First expression: 4r + 8 ≥ 32

Subtract 8 from both sides.

4r ≥ 24

Divide both sides by 4.

r ≥ 6

---

Second expression: 4r + 8 ≤ - 32

Subtract 8 from both sides.

4r ≤ -40

Divide both sides by 4.

r ≤ -10

---

Your answer is
`\boxed {r \geq 6~or~ r \leq -10}`