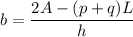Answer:
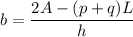
Explanation:
Given : The Kahn's Family lives in a house that has a backyard in the shape of an isosceles trapezoid and a triangle.
The area (A) of the backyard can be expressed as the sum of the area of the triangle and the area of the trapezoid :

, where base and the height of the triangle are represented by b and h, respectively. The bases of the trapezoid are p and q, and the height of the trapezoid is L.
To find the formula for base b, we subtract expression
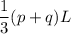 from both sides of the given formula , we get
from both sides of the given formula , we get
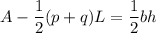
Now, multiply both sides by 2 and divide both sides by h , we get
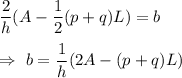
i.e. The formula to find the length of base as a function of the lengths of the other sections of the backyard will be :-