Question

Use the Factor Theorem to show that (x - 3) is a factor of the polynomial

P(x) = x^5-3x^4+5x^3-15x^2-6x+18

Answer 1

P(3) = 0

Explanation:

Factor Theorem is a consequence of Remainder Theorem.

Remainder Theorem states that if polynomial f(x) is divided by a binomial (x - a) then the remainder is f(a).

Factor Theorem states that if f(a) = 0, then the binomial (x - a) is a factor of f(x).

We have the polynomial

`P(x) = x^5-3x^4+5x^3-15x^2-6x+18`

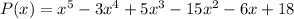
To prove that x-3 is a factor of P, we calculate P(3):

`P(3) = 3^5-3*3^4+5*3^3-15*3^2-6*3+18`

`P(3) = 243-243+135-135-18+18`

`P(3) = 0`

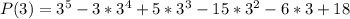
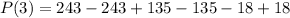
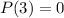
Thus, x-3 is a factor of P(x)