Question

Sandy and Robert each have various polygons in their polygon buckets. Sandy randomly selects a polygon from her polygon bucket and Robert randomly selects a polygon from his.

A. who has a greater probability of selecting a quadrilateral? Justify your conclusion.

B. who has a greater probability of selecting an equilateral polygon? justify your conclusion.

C. what is more likely to happen: Sandy selecting a polygon with at least two sides that are parallel or Robert selecting a polygon with at least two sides that are equal ?

can anyone help me with all this. i would appreciate it very much.

Answer 1

(A)

Number of Quadrilateral in Sandy Bucket =[Square,Rhombus]=2

Number of Quadrilateral in Robert Bucket =[Kite,Quadrilateral]=2

Probability of an event

`=\frac{\text{Total Favorable Outcome}}{\text{Total Possible Outcome}}`

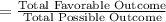
→Probability of Selecting a Quadrilateral by Sandy

`=(2)/(4)\\\\=0.50`

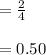
→Probability of Selecting a Quadrilateral by Robert

`=(2)/(5)\\\\=0.40`

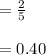
Selecting a Quadrilateral by Sandy has more probability than Selecting a Quadrilateral by Robert.

(B)

Number of equilateral polygon in Sandy's Bag={Square, Equilateral Triangle,Regular Hexagon}

Probability of selecting an equilateral polygon by Sandy

`=(3)/(4)\\\\=0.75`

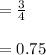
Number of equilateral polygon in Robert's Bag=0

Probability of selecting an equilateral polygon by Robert=0

So, Probability of selecting an equilateral polygon by Sandy is greater than selecting an equilateral polygon by Robert.

(C)

Selecting a polygon with at least two sides that are parallel

={Square, Rhombus,Regular Hexagon}

Selecting a polygon with at least two sides that are equal

={Isosceles Triangle, Right Isosceles Triangle,Kite}

Probability of Selecting a polygon with at least two sides that are parallel out of four geometrical shapes by Sandy

`=(3)/(4)\\\\=0.75`

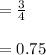
Probability of Selecting a polygon with at least two sides that are parallel out of four geometrical shapes by Robert

`=(3)/(5)\\\\=0.6`

Selecting a polygon with at least two sides that are parallel by Sandy is more likely than Selecting a polygon with at least two sides that are equal by Robert.

Answer 2

we are given that

Sandy and Robert each have various polygons in their polygon buckets. Sandy randomly selects a polygon from her polygon bucket and Robert randomly selects a polygon from his.

A. who has a greater probability of selecting a quadrilateral? Justify your conclusion.

Answer: Sandy has greater proabaility(1/2) because in sandy bucket number of Quadrilaterals are more than the Robert(1/5). Also the number of polygon is less in case of Sandy. Hence greater proabaility for Sandy.

B. who has a greater probability of selecting an equilateral polygon? justify your conclusion.

Answer: Aagain sandy has greater probability because for sandy its 1/4 and for Robert its 1/5.

C. what is more likely to happen: Sandy selecting a polygon with at least two sides that are parallel or Robert selecting a polygon with at least two sides that are equal ?

Answer: Sandy has the probability of
`(2)/(4)=(1)/(2)`, while RFobert has the probability of
`(1)/(5)`. So again sany has greater probability.