Question

Find the slope dy/dx of the polar curve r = 3 / (2 - cos(theta)) at the point (r, theta) = (3/2, pi/2)

Answer 1

Given polar equation is

`r=(3)/(2-\cos\left(\theta\right))`

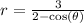
for polar equation we use

`x=r\cos\left(\theta\right)`

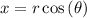
and
`y=r\sin\left(\theta\right)`

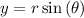
plug the given value of r into these equations we get:

`x=r\cos\left(\theta\right)=(3\cos\left(\theta\right))/(2-\cos\left(\theta\right))`

`y=r\sin\left(\theta\right)=(3\sin\left(\theta\right))/(2-\cos\left(\theta\right))`

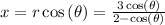
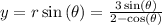
find derivative with respect to theta

`(dx)/(d\theta)=-(6\sin\left(\theta\right))/(\left(2-\cos\left(\theta\right)\right)^2)`

`(dy)/(d\theta)=-(3\left(\sin^2\left(\theta\right)+\cos^2\left(\theta\right)-2\cos\left(\theta\right)\right))/(\left(2-\cos\left(\theta\right)\right)^2)`

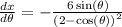
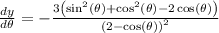
now slope is given by formula

`m=((dy)/(d\theta))/((dx)/(d\theta))`

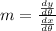
plug the above values into slope formula and the given angle theta = pi/2

`m=(-(3\left(\sin^2\left(\theta\right)+\cos^2\left(\theta\right)-2\cos\left(\theta\right)\right))/(\left(2-\cos\left(\theta\right)\right)^2))/(-(6\sin\left(\theta\right))/(\left(2-\cos\left(\theta\right)\right)^2))`

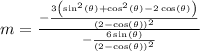
plugging theta=pi/2 and simplifying it gives

m=0.5

Hence final answer is m=0.5