Question

In the diagram, ATPR~AXPZ. Find the length of side PZ.

T
25
15
Х
9
P
s
Y
9
15
N
R
The length of side PZ is

Answer 1

PZ = 15

Explanation:

Similar Triangles

Two triangles are similar if all of their corresponding side lengths are proportional to the same scale factor.

It's given triangles TPR and XPZ are similar, thus we can find the scale factor by comparing two corresponding sides with known lengths.

Sides TR and ZX are corresponding and the proportion of their side lengths is 15/9. The same proportion must be satisfied by the sides TP and XP:

`\displaystyle (15)/(9)=(25)/(PX)`

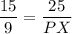
PX and PZ are congruent, thus:

`\displaystyle (15)/(9)=(25)/(PZ)`

`\displaystyle PZ=25*(9)/(15)`

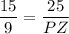
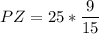
Calculating:

PZ = 15