Answer:
As the lines are neither parallel nor perpendicular.
Therefore, These lines are neither parallel nor perpendicular.
Explanation:
The slope-intercept form of the line equation
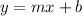
where
Given the lines
y = 3/2x + 2
Finding the slope of y = 3/2x + 2
comparing with the slope-intercept form of the line equation
The slope m₁ = 3/2
y = 2/3x + 6
Finding the slope of y = 2/3x + 6
comparing with the slope-intercept form of the line equation
The slope m₂ = 2/3
So,
m₁ = 3/2
m₂ = 2/3
We know that when two lines are parallel, they have equal slopes
But
m₁ ≠ m₂
3/2 ≠ 2/3
As the m₁ and m₂ are not equal.
Hence, the lines are not parallel.
We know that when two lines are perpendicular, the product of their slopes is -1.
Let us check the product of two slopes m₁ and m₂
m₁ × m₂ = 3/2 × 2/3
= 6/6
= 1
As
m₁ × m₂ ≠ -1
Thus, the lines are not perpendicular.
Conclusion:
As the lines are neither parallel nor perpendicular.
Therefore, These lines are neither parallel nor perpendicular.