Question

8. Find the area of a circle with center

(2, 3) that passes through (2,7)
Use 3.14 for a
F 12.58 units H 41.38 units?
6 25.12 units? J 50.24 units
Pls help

Answer 1

Area of circle = 50.24 units

Option J is correct answer.

Explanation:

We need to find the area of a circle with centre (2, 3) that passes through (2,7)

The formula used to find area of circle is:

`Area\: of\: circle=\pi \:r^2`

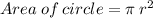
We need to find radius.

The radius can be found using the distance between points (2,3) and (2,7)

The The distance formula is:
`Distance = √((x_2-x_1)^2+(y_2-y_1)^2)`

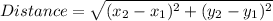
Putting values and finding length

We have:
`x_1=2, y_1=3, x_2=2, y_2=7`

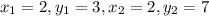
Putting values and finding distance

`Distance = √((x_2-x_1)^2+(y_2-y_1)^2)\\Distance = √((2-2)^2+(7-3)^2)\\Distance = √((0)^2+(4)^2)\\Distance = √(0+16)\\Distance = √(16)\\Distance = 4`

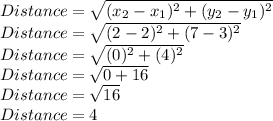
So, we found Distance = 4

Therefore, the radius of circle is 4

Now, finding area:

`Area\: of\: circle=\pi \:r^2\\Area\: of\: circle=3.14* (4) ^2\\Area\: of\: circle=3.14* 16\\Area\: of\: circle=50.24 \:units`

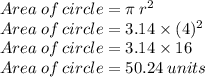
So, Area of circle = 50.24 units

Option J is correct answer.