So with ∠b and ∠a, they are a linear pair, which are adjacent angles that are formed when two lines intersect. Linear pairs are supplementary, which means that they add up to 180 degrees. With our information, we can form the equation
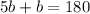(Remember that ∠a = 5b)
Firstly, combine like terms:
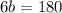
Next, divide both sides by 6 and ∠b = 30 degrees.
Next, to find ∠a, just multiply the value of ∠b (30 degrees) and 5, and ∠a = 150 degrees.
Next, ∠c and ∠a are vertical angles, which are angles that are across from each other that are formed by intersecting lines and are congruent to each other. In this case, since we know that ∠a = 150 degrees, this means that ∠c = 150 degrees.
Next, ∠b and ∠d are vertical angles as well (Refer back to the prior paragraph for definition of vertical angles.). Since ∠b = 30 degrees, ∠d = 30 degrees as well.
Next, ∠a and ∠e are corresponding angles. Corresponding angles are angles that are in the same relative position with each other, are formed when a transversal crosses parallel lines, and are congruent to each other. In this case, ∠a and ∠e are the leftmost angles of their intersections and since ∠a = 150 degrees, ∠e = 150 degrees.
And lastly, ∠b and ∠f are corresponding angles (refer to prior paragraph for more info on corresponding angles). Since ∠b = 30 degrees, ∠f = 30 degrees.