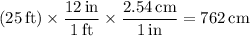6. Multiply the given equation by 20
... 20×1 in. = 20×2.54 cm
... 20 in = 50.8 cm
7. Multiply the equation (1 foot = 12 inches) by 25.
... 25×1 ft = 25×12 in
... 25 ft = 300 in
Now, multiply the equation for conversion to cm by 300
... 300×1 in = 300×2.54 cm
... 300 in = 762 cm
Using the transitive property of equality,
... 25 ft = 300 in = 762 cm
... 25 ft = 762 cm
_____
A "unit multiplier" is no doubt explained in your lesson. We assume it is a fraction whose value is 1, but that has different units in numerator and denominator. The equation 1 in = 2.54 cm gives rise to two unit multipliers, depending on which conversion you need or want:
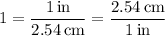
Since you're converting to centimeters, you want the one with cm in the numerator.