Question

Given the points (7,3) ( 7 , 3 ) and (k,−7) ( k , − 7 ) , for which values of k would the distance between the points be 2√ 41 ?

Answer 1

Answer: The required value of k is 15 or -1.

Step-by-step explanation: Given that the distance between the points (7, 3) and (k, -7) is 2√41 units.

We are to find the value of k.

Distance formula : The distance between the points (a, b) and (c, d) is given by

`D=√((c-a)^2+(d-b)^2).`

According to the given information, we have

`√((k-7)^2+(-7-3)^2)=2√(41)\\\\\Rightarrow (k-7)^2+(-10)^2=(2√(41))^2\\\\\Rightarrow (k-7)^2+100=164\\\\ \Rightarrow (k-7)^2=164-100\\\\\Rightarrow (k-7)^2=64.`

Taking square root on both sides, we get

`k-7=8\\\\\Rightarrow k=8+7\\\\\Rightarrow k=15`

or

`k-7=-8\\\\\Rightarrow k=-8+7\\\\\Rightarrow k=-1`

Thus, the required value of k is 15 or -1.

Answer 2

You have to use the distance formula here to figure this one out. The distance formula is

`d=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`.

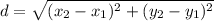We have the distance, we have one of the x-coordinates and both of the y coordinates so we fill in accordingly:

`2√(41)=√((k-7)^2+(-7-3)^2)`

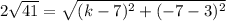
which simplifies to

`2√(41) =√(k^2-14k+49+100)`. What we did there was expand the binomial of (k-7)(k-7). That simplifies even further to

`2√(41)=√(k^2-14k+149)`.

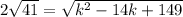Now we have to find a way to solve that for k, which means to get it out from under the square root sign. Since squaring a square root "undoes" the square root AND we have square roots on both sides of the equation, we will square both sides of the equation (which you would have to do anyway since this is an equation and if you do one thing to one side of it you have to do the same thing to the other side!) Squaring both sides,

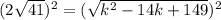`(2√(41))^2=(√(k^2-14k+149))^2`. Since squaring undoes the square roots we now have

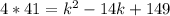`4*41=k^2-14k+149`. Multiplying on the left side and then adding that product to the right side and setting the whole mess equal to 0 gives us

`0=k^2-14k-15`.

Now we just have to factor that in whatever way we deem the most efficient and effective. We can figure what 2 numbers that add together to equal -14 also multiply together to equal -15. Those 2 numbers are k=15 and k=-1. In factorization form that is (k-15)(k+1). Do the FOILing just to see that it's correct and you're good to go!