Question

Which graph models the function f(x)=-2(3)^x

Answer 1

Reflection across x-axis:

`(x, y) \rightarrow (x, -y)`

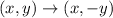
Vertically stretch:

A function y=a f(x) is vertically stretch by a factor a > 1 is that of parent function y=f(x)

Given the graph:
`f(x) = -2(3)^x`

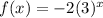
We will make a table values for a few values of x.

then we will graph the given function.

x f(x)

-2 -0.2222..

-1 -0.6666..

0 -2

1 -6

2 -18

3 -54

Note that as x increases, f(x) decreases

Now, using these points (-2, -0.2222..), (-1, -0.666..), (0, -2), (1, -6) , (2, -18) and (3, -54)

Plot the graph of the given function as shown below:

We observe that the curve is that of
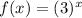`f(x) =(3)^x` except it is vertically stretch by a factor 2 and reflection across x-axis.

Answer 2

`\text{Given: }f(x)=-2(3)^x`

We are an exponential function.

`y=ab^x`

If a<0 and b>1 then graph is decreasing.

If a>0 and b<1 then graph is decreasing.

If a<0 and b<1 then graph is increasing.

If a>0 and b>1 then graph is increasing.

`\text{We have a function }f(x)=-2(3)^x`

Here a=-2<0 and b=3>1 therefore, f(x) is decreasing.

Horizontal asymptote , y=0

x-intercept: Doesn't not exist

y-intercept: (0,-2)

Using above information we will draw the graph f(x)

We make table of x and y for different value of x

x y

-2 -0.22

-1 -0.67

0 -2

1 -6

2 -18

Plot these points on graph and join the points.

Please see the attachment to see the graph.