Question

Use the discriminant to describe the roots of each equation. Then select the best description. 16x2 + 8x + 1 = 0 double root real and rational roots real and irrational roots non-real roots

Answer 1

`16x^2 + 8x + 1 = 0\\\\a=16\qquad b=8\qquad c=1\\\\\\\Delta=b^2-4ac=8^2-4\cdot16\cdot1=64-64=\boxed{0}`

Δ = 0 so we have a double root (answer A).

Answer 2

Explanation:

If a quadratic equation is defined as
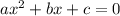`ax^2+bx+c=0`, then the discriminant of the equation is

`D=b^2-4ac`

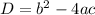
If D>0, then the equation has two real roots, it may be rational or irrational.

If D=0, then the equation has one real root.

If D<0, then the equation has no real roots and 2 complex roots.

The given equation is

`16x^2+8x+1=0`

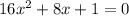
Here, a=16, b=8 and c=1.

The value of the discriminant is

`D=(8)^2^2-4(16)(1)`

`D=64-64`

`D=0`

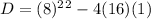
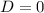
The value of the discriminant is 0, it mean the given equation has two same real root or double root.

Therefore the correct option is 1.