We can say that a relationship between two variables is a function if, for every input, we get one and only one unique output. If we want to talk about y as a function of x in this problem, we want to make sure that every x has only one y associated with it. We can do this by solving our equation for x and seeing whether we can have more than one y that satisfies that equation. Here, I'll do the algebra and briefly explain my steps:
Multiply either side by x to cancel the denominator in 1/x:
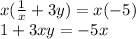
Add 5x to either side to collect all of the x terms on one side, and subtract 1 to get all of the constants on one side:
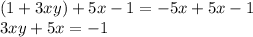
Factor an x out of the left side of the equation:
Divide either side by 3y + 5 to get the x by itself:
For every x we pick, only one y can satisfy the above equation, so we can say that yes,
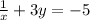is a function.