Question

ALGEBRA 2 ONLY ANSWER 9

Answer 1

The formula of a circle is as follows:

`(x-h)^(2) + (y-k)^(2) = r^(2)`

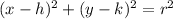
`h` and
`k` stand for the set of coordinates
`(h, k)` which is the center of the circle, and
`r` is the size of the radius.

With the diameter given as
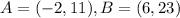`A=(-2, 11), B=(6, 23)` We can find the middle by finding the middle of the x's and the y's. So
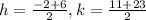`h=(-2+6)/(2), k=(11+23)/(2)`. This simplifies to
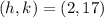`(h, k)=(2, 17)` so our formula currently looks as such:

`(x-2)^(2)+(y-17)^(2)=r^(2)`

Now finding r. Finding the length of a line from point A to point B is
`length=\sqrt{(A_(x)-B_(x))^(2)+(A_(y)-B_(y))^(2)}`

We can plug in our values for A and B as such...

`\sqrt{(-2-6)^(2)+(11-23)^(2)}`

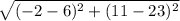
And this simplifies to the length of the diameter, 14.422. To get the radius, simply divide by 2: 7.211, and then square that to find what goes at the very end of the circle formula: 52.

This gives us a final formula of
`(x-2)^(2)+(y-17)^(2)=52`