Question

Jeanine Baker makes floral arrangements. She has 15 different cut flowers and plans to use 5 of them. How many different selections of the 5 flowers are​ possible?

Answer 1

For the first flower she has a choice of 15. For the second 14 (15 minus the one that was already used). For the third 13, and so on.

Each of the first 15 can be match with any of the second 14. Any of the first pairs can be matched with ant of the third 13 and so on.

This gives us

Number of Selections = Choices for Flower 1 x Choices for Flower 2 x Choices for Flower 3 x Choices for Flower 4 x Choices for Flower 5

`N_(s)=f_(1) * f_(2) * f_(3) * f_(4) * f_(5)`

`N_(s)=15 * 14 * 13 * 12 * 11`

`N_(s)=360,360`

You could also calculate this as the permutation
`_(15)P_(5)=(15!)/((15-5)!)`

Answer 2

There are 3003 different ways to choose the 5 flowers.

Explanation:

For solving this question we need to understand the concept of combination. The combination can be calculate as:

`nCk=(n!)/(k!(n-k)!)`

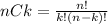
This value give as the number of ways in which we can select k elements from a group of n elements and the order in which this elements are chosen doesn't matter.

Replacing n by 15 and k by 5, we get:

`15C5=(15!)/(5!(15-5)!)`

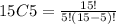
15C5=3003

So, there are 3003 different ways to choose the 5 flowers from a group of 15.