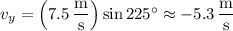Because the speed of the sled is constant throughout this ordeal, we know that the instantaneous and average velocities are equal, and the velocity of the sled is

(negative because we're taking the downward direction to be negative)
The vertical component of this vector is given by
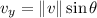
where
 is the angle made by the velocity vector with the positive
is the angle made by the velocity vector with the positive
 -axis (taken to be the right direction). Here,
-axis (taken to be the right direction). Here,
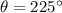 , so
, so