Answer:
B.
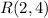
Explanation:
The equation of a circle with center
 and the radius,
and the radius,
 , is
, is
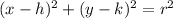
Here, the center of the circle is at
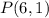 and the radius of the circle is 5 units.
and the radius of the circle is 5 units.
So,
 and
and
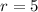
Therefore, the equation of the circle is

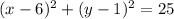
Now, the point that satisfies the equation of the circle will lie on the circle.
Let us take all the points one by one.
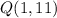
 , which is incorrect.
, which is incorrect.
So,
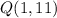 does not lie on the circle.
does not lie on the circle.
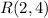
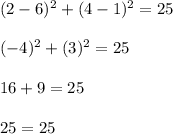 , which is correct.
, which is correct.
So,
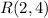 lie on the circle.
lie on the circle.
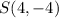
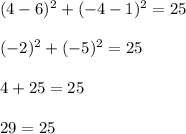 , which is incorrect.
, which is incorrect.
So,
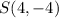 does not lie on the circle.
does not lie on the circle.
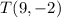
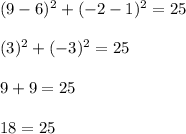 , which is incorrect.
, which is incorrect.
So,
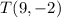 does not lie on the circle.
does not lie on the circle.
Hence, the point
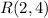 lie on the circle.
lie on the circle.