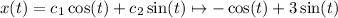Question

In this problem, x = c1 cos t + c2 sin t is a two-parameter family of solutions of the second-order de x'' + x = 0. find a solution of the second-order ivp consisting of this differential equation and the given initial conditions. x(0) = −1, x'(0) = 3

Answer 1

If you are already given the general solution, finding the particular solution means to impose some conditions in order to fix the coefficients of the general solution.

The first thing we need to impose is that the function must output -1 when the input is zero. So, if we plug zero as input we have

`x(t) = c_1 \cos(t) + c_2 \sin(t) \implies x(0) = c_1 \cos(0) + c_2 \sin(0) = c_1`

But we want
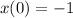`x(0)=-1`, which implies
`x(0)=c_1=-1`

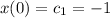
So, we fixed the first coefficient. To fix the second one, we can use the second piece of information (and of course the already-found value for
`c_1`).

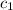We want the first derivative to output 3 when the input is zero. So, first of all, let's compute the first derivative, and evaluate it in zero:

`x(t) = -\cos(t) + c_2 \sin(t) \implies x'(t) = \sin(t) + c_2\cos(t)`

`x'(0) = \sin(0) + c_2\cos(0) = c_2`

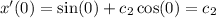
And as before, since
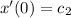`x'(0)=c_2` and we want
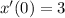`x'(0)=3`, we deduce
`c_2=3`.

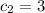So, once we fix both coefficients, the general solution becomes

`x(t) = c_1 \cos(t) + c_2 \sin(t) \mapsto -\cos(t)+3\sin(t)`