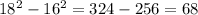As the exercise suggests, let's call the two consecutive integers
 and [/tex] x+2 [/tex]. In fact, if
and [/tex] x+2 [/tex]. In fact, if
 is even, the next number,
is even, the next number,
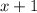 is odd, and the next number
is odd, and the next number
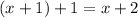 is again even.
is again even.
Moreover, since the two numbers are positive, the square of the bigger one is actually bigger, so the difference is
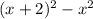
In fact, note that if the numbers were negative, for example -6 and -4, their squares would be 36 and 16, so you should have subtracted
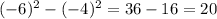
So, the difference of their squares is
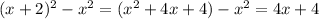
And we know that this difference is 68, so the equation is
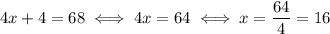
So, the two consecutive even integers are 16 and 18.
Let's check the answer!
The difference of their squares is