What are the domain range and asymptote of h(x)=6^x-4

Question

asked Mar 16, 2019 85.5k views

1 Answer

Jeroen Heier · Answer 1 · 2019-03-20T02:34:29+0000

The asymptote of the function f(x) = aˣ is y = 0.

The domain of the function f(x) = aˣ is x ∈ R.

The range of the function f(x) = aˣ is y > 0.

-----------------------------------------------------------------------------------

f(x - n) - shifting the graph by n units to the right

f(x + n) - shifting the graph by n units to the left

f(x) - n - shifting the graph by n units down

f(x) + n - shifting the graph by n units up

---------------------------------------------------------------------------

We have
h(x)=6^(x-4)

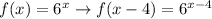$f(x)=6^x\to f(x-4)=6^(x-4)$ - shifting the graph of f(x) = 6ˣ, 4 units to the right. Therefore

Domain - no change

Range - no change

Asymptote - no change

Answer:

The asymptote is y = 0. The domain is x ∈ R. The range is y > 0.

If
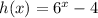h(x)=6^x-4 , therefore

$f(x)=6^x\to f(x)-4=6^x-4$ - shifting the graph of f(x) = 6ˣ, 4 units down.

Therefore, yor answer is:

Domain - no change (x ∈ R)

Range - change → y > -4

Asymptote - change → y = -4