Question

Line segment PQ is shown on a coordinate grid: (see image below) The line segment is rotated 270 degrees counterclockwise about the origin to form P'Q'. Which statement describes P'Q'?

Answer 1

It will be B equal in length cause by just rotating it. It will not change the length and your final image with not be parallel sooner or later they will touch if they go on

Answer 2

Answer: The correct option is

(B) P'Q' is equal in length to PQ.

Step-by-step explanation: Given that line segment PQ is shown on the co-ordinate grid. The line segment PQ is rotated 270 degrees counterclockwise about the origin to form P'Q'.

We are to select the statement that describes P'Q'.

From the graph, we note that

the co-ordinates of point P are (-5, 3) and the co-ordinates of Q are (-1, 3).

So, the length of PQ as calculated using distance formula is given by

`PQ=√((-1+5)^2+(-3+3)^2)=√(4^2+0^2)=4~\textup{units}.`

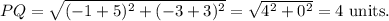
We know that if a point is rotated 270 degrees counterclockwise, then its co-ordinates changes as follows :

(x, y) → (y, -x).

So, after the rotation, the co-ordinates of P and Q becomes

P(-5, 3) → P'(3, 5)

Q(-1, 3) → Q'(3, 1).

The length of the line segment P'Q' as calculated using distance formula is

`P'Q'=√((3-3)^2+(1-5)^2)=√(4^2)=4~\textup{units}.`

Thus, the lengths of PQ and P'Q' are equal.

Option (B) is CORRECT.