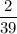Question

A mini bag of Skittles has 3 lemon, 4 grape, 4 orange and 2 lime Skittles. What is the probability of randomly pulling an orange Skittle out first and eating it and then pulling a lime Skittle out of the bag next?

Answer 1

I think that the answer would be 2 out of 36 chance or 1 in 18 chance.

Answer 2

Answer:
`(2)/(39)`

Explanation:

Given : A mini bag of Skittles has 3 lemon, 4 grape, 4 orange and 2 lime Skittles.

Total Skittles = 3+4+4+2=13

Probability of pulling an orange Skittle out first : P(First orange)
`=\frac{\text{No. of orange skittles}}{\text{Total skittles}}`

`=(4)/(13)`

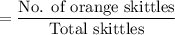
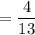
Since the second skittles is drawn without replacement , so after drawing one skittle , the remaining skittles = 13-1=12

So , P(Second skittle is lime) =
`\frac{\text{No. of lime Skittles}}{\text{remaining skittles }}`

`=(2)/(12)=(1)/(6)`

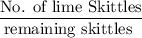
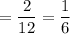
Since the events of pulling any Skittle are independent .

So , P( Orange then lime)= P(First orange) x P(Second skittle is lime)

`=(4)/(13)*(1)/(6)=(2)/(39)`

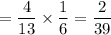
∴ The probability of randomly pulling an orange Skittle out first and eating it and then pulling a lime Skittle out of the bag next =
`(2)/(39)`