Answer:
A)
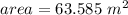 ,
,
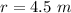
B)
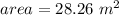 ,
,
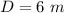
C)
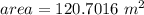 ,
,

D)
 ,
,
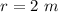
E)
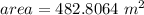 ,
,
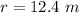
F)
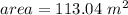 ,
,
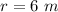
Explanation:
we know that
The area of a circle is equal to
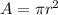
solve for r
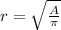
Verify each case
case A)
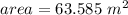
substitute in the formula

case B)
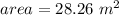
substitute in the formula
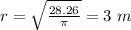
the diameter is equal to
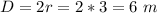
case C)
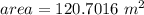
substitute in the formula
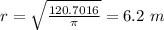
the diameter is equal to
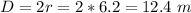
case D)

substitute in the formula
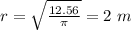
case E)
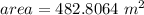
substitute in the formula
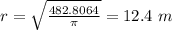
case F)
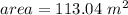
substitute in the formula
