Question

In two or more complete sentences, describe the transformation(s) that take place on the parent function, f(x) = log(x), to achieve the graph of g(x) = log(-3x-6) - 2.

Answer 1

log(2x)=4

log2⁢x=4 in exponential form using the definition of a logarithm. If

x x and b b are positive real numbers and b ≠ 1, then log b(x)=y logbx=y is equivalent to by=x. 10 4 = 2x

hope it helps

Answer 2

Answer and explanation:

Given : The transformation(s) that take place on the parent function
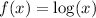`f(x) = \log(x)` to achieve the graph of
`g(x) = \log(-3x-6) - 2`.

To find : Describe the transformation(s) ?

Solution :

Parent function
`f(x) = \log(x)`

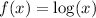
1) Translate the graph of function to horizontally compress

i.e. f(x)→f(ax), a>0

So,
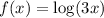`f(x) = \log(3x)` i.e. horizontally compress with 3 units.

2) Translate the graph of function to the left with a unit

i.e. f(x)→f(x+a)

So,
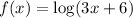`f(x) = \log(3x+6)` i.e. Horizontal shift left with 6 units.

3) Translate the graph of function to the down with b unit

i.e. f(x)→f(x)-b

So,
`f(x) = \log(3x+6)-2` i.e. Vertical shift down with 2 units.

4) Translate the graph of function by reflection about the y-axis

i.e. f(x)→f(-x)

So,
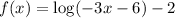`f(x) = \log(-3x-6)-2` i.e. Reflection about the y-axis.