Question

What are the solutions of the equation x^2 + 4x + 4= 25?

a. x = 3 or x = -7
b. x = -3 or x = 7
c. x = 1 or x = 9
d. x = 1 or x = -9

Answer 1

Firstly, you need to set the equation to 0. To do that, subtract both sides by 25:
`x^2+4x-21=0` .

Next, we can complete the square. But first, what two terms have a product of -21x^2 and a sum of 4x? That would be 7x and -3x. Replace 4x in the equation with 7x - 3x:
`x^2 +7x-3x-21=0`

Next, factor x^2 + 7x and -3x - 21 separately. Make sure that they both have the same quantity on the inside:
`x(x+7)-3(x+7)=0`

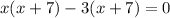
Now you can rewrite the equation as
`(x-3)(x+7)=0`

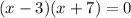
Now using zero product property, solve for x:

`x-3=0\\ x=3\\ \\ x+7=0\\ x=-7`

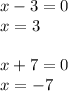
In short, your answer is A. x = 3 or x = -7.