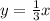Question

A direct variation function contains the points (–9, –3) and (–12, –4). Which equation represents the function?

Answer 1

A direct variation equation is one that requires y varies directly as x and looks like this in equation form:

`(y)/(x) =k`

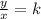
where k is the constant of variation. If we solve this for y, we have y = kx, which happens to be a linear function... a line. k here, then, serves as the slope. So what we are given as points on a direct variation function are actually points on a line. The equation for this requires that we find the slope and then rewrite the formula accordingly. First the slope:

`m(k)=(-4-(-3))/(-12-(-9))=(-4+3)/(-12+9)=(1)/(3)`

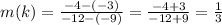
Now we need to write the equation by using one of the points' coordinates. I picked the first point that has an x coordinate of -9 and a y coordinate of -3. Fitting those into the slope-intercept form of a line,

`-3=(1)/(3)(-9)+b`

which simplifies to

-3 = -3 + b and b = 0. That means that the equation of direct variation is

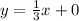`y=(1)/(3)x+0` or just

`y=(1)/(3)x`

Answer 2

The answer is y=x/3 hope this helps.