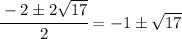Question

Solve for x in the equation x^2 + 2x + 1 = 17

Answer 1

If you subtract 17 from both sides, the equation becomes

`x^2+2x-16 = 0`

and it's a quadratic equation in standard form, i.e.
`ax^2+bx+c=0`

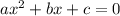
If you name the coefficients like this, the equation has solutions

`x_(1,2) = \cfrac{-b\pm√(b^2-4ac)}{2a}`

So, if you plug your values for a,b and c you have

`x_(1,2) = \cfrac{-2\pm√(4-4\cdot 1 \cdot (-16))}{2\cdot 1} = \cfrac{-2\pm√(68)}{2}`

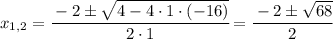
Since 68 = 4 x 17, we have

`√(68) = √(4* 17) = √(4)√(17) = 2√(17)`

So, the solutions can be written as

`\cfrac{-2\pm2√(17)}{2} = -1\pm √(17)`

Answer 2

Option(B) is the answer
Hope this helps you..!!