Y has a coefficient of 1 in the first equation, so it is easiest to use that one to write an expression for y.
... y = 20 - 2x . . . . . subtract 2x
Now, this expression can be substituted for y in the second equation.
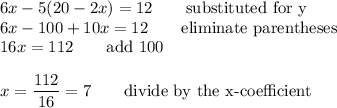
Then, using the expression for y, we find its value
... y = 20 -2·7 = 6
The solution of the equations is (x, y) = (7, 6).