Answer:
Range:
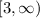
Explanation:
We have been given a function
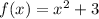 . We are asked to find the range of our given function.
. We are asked to find the range of our given function.
We know that range of a function is values of dependent variable (y) for which function is defined.
We can see that our given parabola is in vertex form
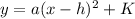 as
as
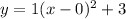 with a vertex at point
with a vertex at point
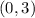 .
.
Since our given parabola is an upward opening parabola, so point
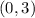 is the minimum point.
is the minimum point.
We know that the range of an exponential function is form
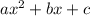 with a vertex at (h,k) is:
with a vertex at (h,k) is:
If
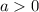 , then range is
, then range is
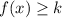
If
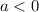 , then range is
, then range is
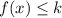
Since the value of a is positive and
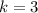 , therefore, the range of our given function would be
, therefore, the range of our given function would be
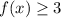 that is
that is
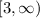 .
.