Product of Slope of a line and its perpendicular is -1.
Suppose slope of a line is m1 and its perpendicular is m2.
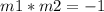
The general slope intercept form is given by :

We are given the equation,

Comparing our equation with general slope intercept form , we have
slope (m1) = -3
slope of line perpendicular to it (m2) is given by formula above
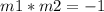
plugging m1=-3 in this
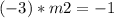
dividing both sides by -3,
m2 =1/3
So slope of line perpendicular to given line is 1/3.