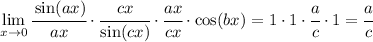Let's break down the fraction into multiple factors:
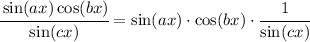
Now we will manipulate the expression (multiply and divide by the same quantitues) in order to be able to use the known limit
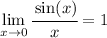
Here's the manipulated expression:
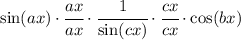
Rewrite the expression as
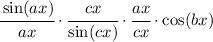
The first two factors tend to 1, because that's the limit we mentioned before. The third factor is simply a/c, because the x's cancel out. Finally, we have
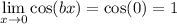
So, the final answer is