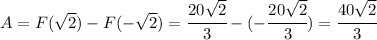Question

Farmer jones, and his wife, dr. jones, decide to build a fence in their field, to keep the sheep safe. since dr. jones is a mathematician, she suggests building fences described by y=6x2 and y=x2+10. farmer jones thinks this would be much harder than just building an enclosure with straight sides, but he wants to please his wife. what is the area of the enclosed region? 42.164

Answer 1

Consider the attached figure (note that the axis are not in a 1:1 scale).

We want the (finite) area between the two parabolas, where
`y = 6x^2` is the green one, and
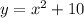`y = x^2+10` is the red one.

We need the following result: given a function f, the integral

`\displaystyle \int_a^b f(x)\; dx`

returns the area between the function and the x axis.

So, if we subtract the area below the green function between points A and B from the area below the red function between points A and B, we have exactly the area between the two. So, we need the x coordinates of points A and B.

Since they are the points of interception between the two parabolas, we can compute them by solving the equation

`6x^2 = x^2+10 \implies 5x^2=10\implies x^2=2 \implies x=\pm√(2)`

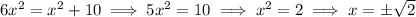
So, we need

`\displaystyle \int_(-√(2))^(√(2)) (x^2+10)-6x^2 = \int_(-√(2))^(√(2)) -5x^2+10`

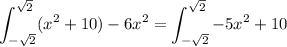
The primitive of this function is

`F(x) = -\cfrac{5x^3}{3} + 10x + C`

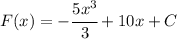
And we need to compute it at the two endpoints: the area is given by

`A = F(√(2)) - F(-√(2)) = \cfrac{20√(2)}{3} - (- \cfrac{20√(2)}{3}) = \cfrac{40√(2)}{3}`