Question

Find an equation of the sphere with center (2, −10, 3) and radius 5. $$25=(x−2)2+(y−(−10))2+(z−3)2 use an equation to describe its intersection with each of the coordinate planes. (if the sphere does not intersect with the plane, enter dne.)

Answer 1

In the
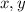`x,y` plane, we have
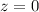`z=0` everywhere. So in the equation of the sphere, we have

`25=(x-2)^2+(y+10)^2+(-3)^2\implies(x-2)^2+(y+10)^2=16=4^2`

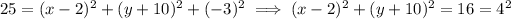
which is a circle centered at (2, -10, 0) of radius 4.

In the
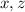`x,z` plane, we have
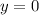`y=0`, which gives

`25=(x-2)^2+10^2+(z-3)^2\implies(x-2)^2+(z-3)^2=-75`

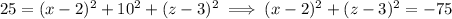
But any squared real quantity is positive, so there is no intersection between the sphere and this plane.

In the
`y,z` plane,
`x=0`, so

`25=(-2)^2+(y+10)^2+(z-3)^2\implies(y+10)^2+(z-3)^2=21=(√(21))^2`

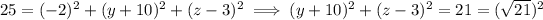
which is a circle centered at (0, -10, 3) of radius
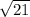`√(21)`.