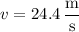Question

Consult interactive solution 2.22 before beginning this problem. a car is traveling along a straight road at a velocity of +30.0 m/s when its engine cuts out. for the next 2.46 seconds, the car slows down, and its average acceleration is . for the next 6.79 seconds, the car slows down further, and its average acceleration is . the velocity of the car at the end of the 9.25-second period is +15.2 m/s. the ratio of the average acceleration values is = 1.66. find the velocity of the car at the end of the initial 2.46-second interval.

Answer 1

Let
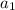`a_1` be the average acceleration over the first 2.46 seconds, and
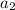`a_2` the average acceleration over the next 6.79 seconds.

At the start, the car has velocity 30.0 m/s, and at the end of the total 9.25 second interval it has velocity 15.2 m/s. Let
`v` be the velocity of the car after the first 2.46 seconds.

By definition of average acceleration, we have

`a_1=(v-30.0\,(\mathrm m)/(\mathrm s))/(2.46\,\mathrm s)`

`a_2=(15.2\,(\mathrm m)/(\mathrm s)-v)/(6.79\,\mathrm s)`

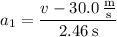
and we're also told that

`(a_1)/(a_2)=1.66`

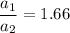
(or possibly the other way around; I'll consider that case later). We can solve for
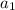`a_1` in the ratio equation and substitute it into the first average acceleration equation, and in turn we end up with an equation independent of the accelerations:

`1.66a_2=(v-30.0\,(\mathrm m)/(\mathrm s))/(2.46\,\mathrm s)`

`\implies1.66\left((15.2\,(\mathrm m)/(\mathrm s)-v)/(6.79\,\mathrm s)\right)=(v-30.0\,(\mathrm m)/(\mathrm s))/(2.46\,\mathrm s)`

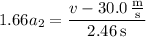
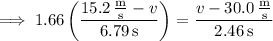
Now we can solve for
`v`. We find that

`v=20.8\,(\mathrm m)/(\mathrm s)`

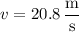
In the case that the ratio of accelerations is actually

`(a_2)/(a_1)=1.66`

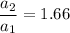
we would instead have

`(15.2\,(\mathrm m)/(\mathrm s)-v)/(6.79\,\mathrm s)=1.66\left((v-30.0\,(\mathrm m)/(\mathrm s))/(2.46\,\mathrm s)\right)`

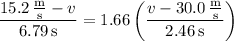
in which case we would get a velocity of

`v=24.4\,(\mathrm m)/(\mathrm s)`