So the equation for finding the outliers is
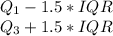
Firstly, however, we need to find the IQR (Q3-Q1), the lower quartile (Q1) and the upper quartile (Q3). Firstly, rearrange the data so that everything is in order: {40,43,44,45,46,50,51,54,56,58,60,62,65,66,68,99}
Next, find the median, which in this case its in between 54 and 56, so the average of the 2 is 55, which makes it the median.
Next, find the "median" of the data from 40-54, aka the lower quartile. In this case, the lower quartile is in between 45 and 46, and the average of the 2 is 45.5. 45.5 is our lower quartile.
Next, find the "median" of the data from 56-99, aka the upper quartile. In this case, the upper quartile is in between 62 and 65. The average of the 2 is 63.5, hence making that the upper quartile.
Now that we have the upper and lower quartile, subtract the two to get the IQR: 63.5 - 45.5 = 18. 18 is our IQR.
Now that we have everything, use the equations I had mentioned and solve them:
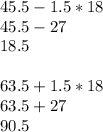
Interpreting these answers, any number that is below 18.5 or above 90.5 is considered an outlier. In our data, the only number that is outside this range is 99, hence making that the only outlier.