Question

What is the rule for the following sequence: 2, 9, 21, 65

Answer 1

There is no common ratio or common difference. The first three terms increases more slowly than a cubic, but the last three increase more quickly than the cube of n. The pattern is not obvious to me. When the sequence is cast in recursive terms, you get

... a[n] = (48/13)a[n-2] + (59/39)a[n-1] . . . . a[1] = 2, a[2] = 9

The next term using this rule is 174 34/39, not an integer.

The coefficients p and q for a[n-2] and a[n-1] can be found from

`2p+9q=21\\9p+21q=65`

_____

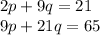
Any sequence of 4 numbers can be matched by a polynomial of degree 3 or less. Here, a calculator's polynomial regression function tells us the rule could be

... a[n] = 4.5n³ -24.5n² +49n -27

Using this rule, the next two terms are 168 and 357.