Question

If you start with 227.8 grams of iron and 128 grams of oxygen to produce iron oxide, what is the limiting reagent?

Answer 1

The balanced chemical equation between iron and oxygen to produce iron (III) oxide is,

`4Fe(s) + 3O_(2)(g) ---> 2Fe_(2)O_(3)(s)`

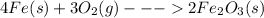
Mass of Fe = 227.8 g

Moles of Fe =
`227.8 g Fe * (1 mol Fe)/(55.85 g Fe) = 4.079 mol Fe`

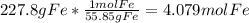
Mass of oxygen = 128 g

Moles of
`O_(2) = 128 g O_(2)*(1 mol O_(2))/(32 g O_(2))= 4mol O_(2)`

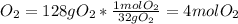
Calculating the limiting reactant: The reactant that produces the least amount of product will be the limiting reactant.

Mass of iron (III) oxide produced from Iron =
`4.079 mol Fe * (2 mol Fe_(2)O_(3))/(4 mol Fe) *(159.69 g Fe_(2)O_(3))/(1 mol Fe_(2)O_(3)) = 325.7 g Fe_(2)O_(3)`

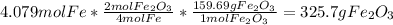
Mass of iron (III) oxide produced from oxygen=
`4 mol O_(2)*(2 molFe_(2)O_(3))/(3 mol O_(2))*(159.69 g Fe_(2)O_(3))/(1 mol Fe_(2)O_(3)) = 425.84 g Fe_(2)O_(3)`

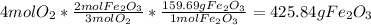
Iron (Fe) produces the least amount of the product iron (III) oxide. So, Fe is the limiting reactant.